https://www.acmicpc.net/problem/17142
17142번: 연구소 3
인체에 치명적인 바이러스를 연구하던 연구소에 승원이가 침입했고, 바이러스를 유출하려고 한다. 바이러스는 활성 상태와 비활성 상태가 있다. 가장 처음에 모든 바이러스는 비활성 상태이고
www.acmicpc.net
조합과 BFS가 짬뽕된 문제. 바이러스를 놓을 수 있는 위치들에 대한 m개의 조합들을 하나하나 살펴보며 BFS를 돌려 판별하면 된다.
이 문제에선 고려해야 할 사항이 좀 더 있다. 바로 BFS의 종료조건.
https://www.acmicpc.net/problem/7576
7576번: 토마토
첫 줄에는 상자의 크기를 나타내는 두 정수 M,N이 주어진다. M은 상자의 가로 칸의 수, N은 상자의 세로 칸의 수를 나타낸다. 단, 2 ≤ M,N ≤ 1,000 이다. 둘째 줄부터는 하나의 상자에 저장된 토마토
www.acmicpc.net
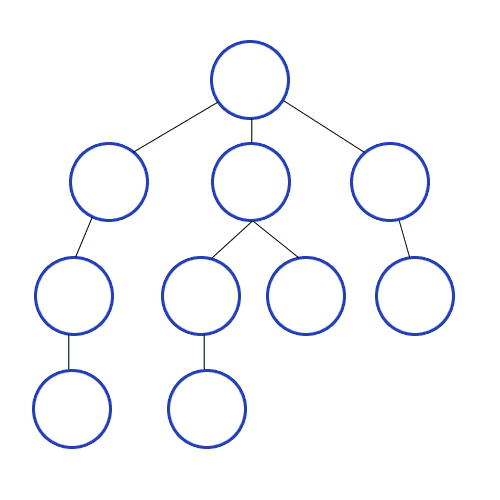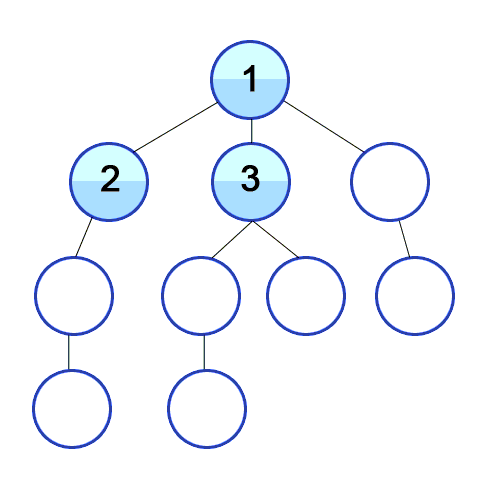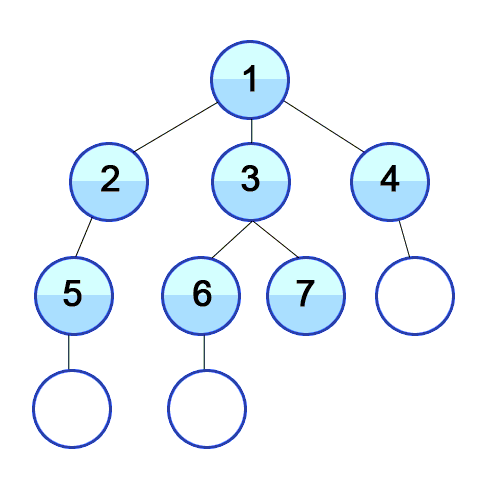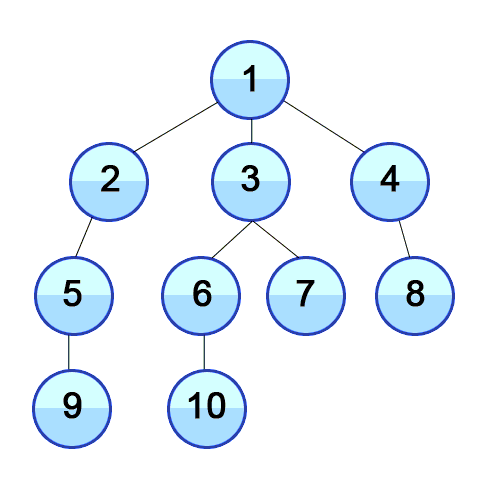
위 문제 "토마토"는 본 문제인 "연구소 3"과 꽤나 유사하다. 익은 토마토가 매 페이즈마다 주변 토마토를 익게 하듯이, 본 문제에서의 바이러스도 매 페이즈마다 주변 칸들에 퍼져 나간다. 또한 모든 토마토가 익을 때까지 최소 며칠이 걸리는지 계산하는 것과 빈 칸이 모두 바이러스가 퍼질 때까지 최소 얼마나 걸리는지를 요구하는 것도 비슷하다.
그러나 디테일에 차이가 있다. 토마토 문제는 모든 토마토가 익을 때까지 BFS를 돌려야 한다면, 본 문제는 빈 칸에 바이러스가 채워질 때까지만 BFS를 돌려야 한다. 즉 벽을 제외한 모든 칸이 활성 바이러스로 채워질 때까지 돌리는 게 아니다. 비활성된 바이러스가 있어도 다른 빈 칸들이 남아있지 않다면 더 이상 BFS를 돌릴 필요가 없다.
따라서 안 익는 토마토가 있든 없든 일단 Queue가 빌 때까지 BFS를 돌려 가능한 모든 구역의 토마토가 익게 한 다음, Queue가 비고 나면 그제서야 모든 토마토가 익어도 되는지 판단해도 되는 토마토 문제와는 달리, 본 문제는 BFS를 돌릴 때마다 연구소 상황을 체크해야 한다. (무작정 큐가 빌 때까지 돌리면 빈 칸들이 다 찰 때까지가 아니라 벽을 제외한 모든 칸에 활성 바이러스가 퍼질 때까지를 보게 되는 문제로 바뀌니까)
즉 빈칸들을 채울 때마다 카운트해주고, 매 BFS마다 현재까지 채운 빈칸의 수와 처음에 셌던 빈칸의 수가 일치하는지를 판단해야 한다. 즉 큐에서 꺼낸 노드마다 상하좌우 네 방향에 대해 방문여부를 확인하고 방문여부를 안 했고 그 칸이 빈칸이면 채운 빈칸의 수를 하나 늘리면 된다.
내가 실수한 부분은, 빈칸을 채운 뒤 채운 빈칸의 수를 늘리는 작업과 빈 칸을 다 채웠는지 판단하는 작업을 동시에 안 했다는 거다. 나는 BFS를 할 때 보통 종료조건을 판단하는 작업을 큐에서 노드를 꺼내고 난 바로 다음에 한다. 얘를 들어 지금 꺼낸 노드가 도착지점이라면 지금까지 카운트한 수가 정답이다! 처럼 판단하는 것. 즉 이 문제는 이런 습관에 따라 처음에 다음과 같이 BFS코드를 짰다.
while q:
1. 만약 지금까지 채운 빈칸의 수가 처음에 센 빈칸의 수와 같다면 종료하는 코드
2. 인접한 칸들이 빈 칸이고 방문하지 않았다면 그 칸을 방문처리하고 큐에 추가한 다음
지금까지 채운 빈칸 수를 += 1
빈칸을 채우고 채운 빈칸 수를 늘리는 작업(2)과 빈칸을 다 채웠는지 판단하는 작업(1)을 동시에 하고 있지 않는 모습이다. 이 때문에 오답이 날 수 있다. 큐에서 노드를 하나 꺼냈는데 x초에 방문한 노드였고, 이 노드의 인접한 빈칸을 채우고 채운 빈칸 수를 늘렸다. 큐에서 다음 노드를 빼냈고 똑같이 x초에 방문한 노드인데, (1)에 의해 지금껏 채운 빈칸 수가 처음에 센 빈칸의 수와 같아 x초에 모든 빈칸을 채웠다고 오답을 뱉게 된다. 사실 x + 1초에 모든 빈 칸이 채워지는 건데 말이다. 만약 임의의 시간 x초에 방문하는 모든 노드들이 방문하지 않은 인접한 빈 칸을 하나 이상씩 가지고 있는게 보장된다면 이런 일은 안 생기겠지만, x초에 방문하는 모든 노드가 방문하지 않은 인접한 빈칸을 가지고 있다는 보장이 없으니 이런 상황이 생긴다.
난 그래서 처음에 틀렸다..ㅋㅋㅋㅋㅋ
암튼..! 빈칸을 채우고 채운 빈칸 수를 늘리는 작업과 빈칸을 다 채웠는지 판단하는 작업을 동시에 해야 한다. 다음과 같이 바꿀 수 있을 것이다.
while q:
1. 지금 꺼낸 노드가 빈 칸이면 지금껏 채운 빈 칸의 수 += 1
2. 만약 지금까지 채운 빈칸의 수가 처음에 센 빈칸의 수와 같다면 종료
3. 인접한 칸들이 빈 칸이고 방문하지 않았다면 그 칸을 방문처리하고 큐에 추가
또는 다음과 같이도 가능하다. 중요한 건 동시에 두 작업을 순서대로 해야 한다는 거.
while q:
1. 꺼낸 노드에 인접한 칸들이 빈 칸이고 방문하지 않았다면 그 칸을 방문처리하고 큐에 추가한 다음
지금까지 채운 빈칸 수를 += 1
2. 지금까지 채운 빈칸 수가 처음에 센 빈칸 수와 같다면 종료. 단 이 작업은 1이 이루어지고 난 이후에만 진행
전체 코드는 다음과 같다.
from itertools import combinations
from collections import deque
import sys
input = sys.stdin.readline
def solution(n, m, board):
directions = [(-1, 0), (0, 1), (1, 0), (0, -1)]
empty_count = 0
virus = []
for r in range(n):
for c in range(n):
if board[r][c] == 2:
virus.append((r, c))
elif board[r][c] == 0:
empty_count += 1
answers = []
for activate_viruses in combinations(virus, m):
q = deque([])
visited = set()
for r, c in activate_viruses:
q.append((r, c, 0))
visited.add((r, c))
empty_to_virus_count = 0
while q:
r, c, h = q.popleft()
if board[r][c] == 0:
empty_to_virus_count += 1
if empty_to_virus_count == empty_count:
answers.append(h)
break
for dr, dc in directions:
nr, nc = r + dr, c + dc
if nr < 0 or nc < 0 or nr >= n or nc >= n:
continue
if board[nr][nc] != 1 and (nr, nc) not in visited:
visited.add((nr, nc))
q.append((nr, nc, h + 1))
if answers:
return min(answers)
return -1
N, M = map(int, input().split())
_board = [list(map(int, input().split())) for _ in range(N)]
print(solution(N, M, _board))
이 문제를 통해 얻은 것.
"다음 노드들에 대한 작업과 종료여부를 판단하는 작업은 동시에 할 것"
'ALGORITHM > 백준BOJ풀이' 카테고리의 다른 글
| [백준] 2504 - 괄호의 값 분할정복 풀이 (python) (0) | 2023.03.20 |
|---|---|
| [백준] 14890 - 경사로 (by 파이썬) (1) | 2023.02.28 |
| [백준] 2075 - N번째 큰 수 (1) | 2023.01.27 |
| [백준] 1026 - 보물 풀이 및 그리디 정당성 검증 (0) | 2022.03.17 |
| [백준] 11726 - 2 x n 타일링 파이썬 풀이 (0) | 2022.02.12 |