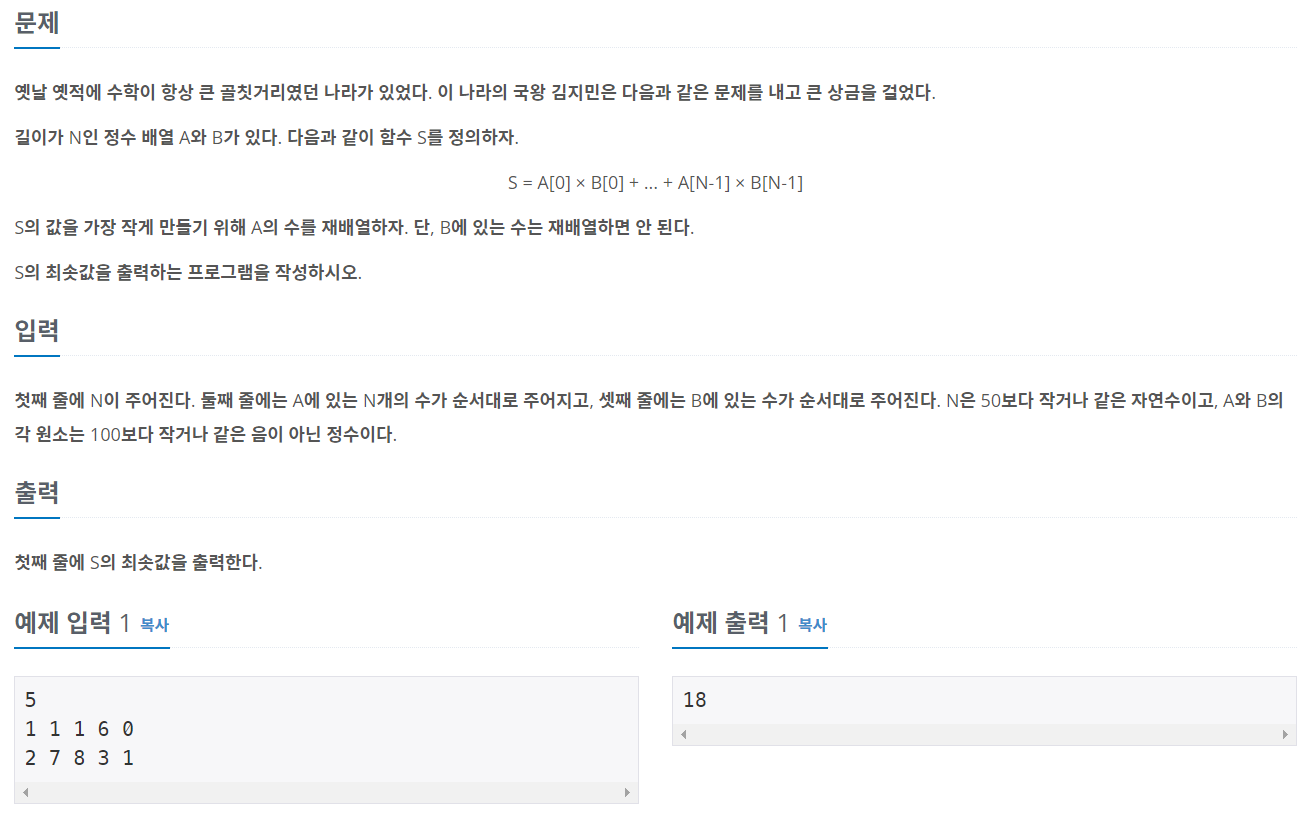
길이가 같은 두 배열 A, B에 대해
S = A의 같은 인덱스항들의 곱들의 합
으로 정의할 때, B를 건드리지 않고 A의 순서만 건드려서 S의 최솟값을 찾는 문제.
무식하게 풀려면 A를 나열하는 모든 경우의 수 = N!개에 대해 따져야 하니 타임아웃.
단순히 A만을 오름차순 / 내림차순 하면 어떨까라고 생각해봤으나 B가 어떤 순서로 주어지는지 알 길이 없기 때문에 이것 역시 적절한 방법이 아니었다.
이에 대한 해결은 A는 오름차순, B는 내림차순으로 정렬해 각 항의 곱들의 합을 구하는 것.
곱해서 나오는 값들의 수를 최대한 작게 나오게 하는 게 관건이므로 A의 가장 작은 값을 B의 가장 큰 값과 짝지어주고, 또다시 남은 A의 가장 작은 값을 남은 B의 가장 큰 값과 짝짓는 과정을 반복해야 하므로 B도 내림차순으로 정렬할 필요가 있다.
뭐 정말 나는 B를 건드리기 싫다! 하면 A만 정렬하고 매번 B의 max값을 찾아 매치해줄 수 있지만 굳이 그럴 필요 없이 B도 정렬해주면 될 것 같다는 생각에서 했다.
정당성 증명 - 왜 가장 작은 값과 큰 값을 매칭해야 하는가
B를 내림차순으로 일단 한 상황에서, A를 왜 가장 작은 값부터 매칭시켜줘야 하는가.
a1과 a2, b1과 b2라는 수가 있고 a1 >= a2, b1 > b2라고 하자. 이 때 주어진 논제를 귀류법으로 증명하기 위해
a2b1 + a1b2이 a1b1 + a2b2보다 작다고 해보자. 우리가 원하는 건 a1b1 + a2b2 >= a2b1 + a1b2임을 보이는 것이다.
뭐 복잡하게 생각할 것 없이, 그냥 이항해서 정리하면 (a1 - a2)b1 >= (a1 - a2)b2임을 보여야 하는 상황이 되는데, 양변을 (a1 - a2)로 나누면 b1 >= b2가 되는데 문제의 조건상 b1 > b2이므로 참이다. 이로써 증명 끝.
곱의 합을 구할 땐 가장 큰 값끼리 곱해준 게 제일 큰 답이 나온다.
'ALGORITHM > 백준BOJ풀이' 카테고리의 다른 글
| [백준] 14890 - 경사로 (by 파이썬) (1) | 2023.02.28 |
|---|---|
| [백준] 2075 - N번째 큰 수 (0) | 2023.01.27 |
| [백준] 11726 - 2 x n 타일링 파이썬 풀이 (0) | 2022.02.12 |
| [백준] 13305 - 주유소 풀이 (0) | 2022.02.09 |
| [백준] 13164 - 행복 유치원 파이썬 풀이, 자세한 풀이와 함께 (0) | 2022.01.29 |