Ray`s Tech Lab

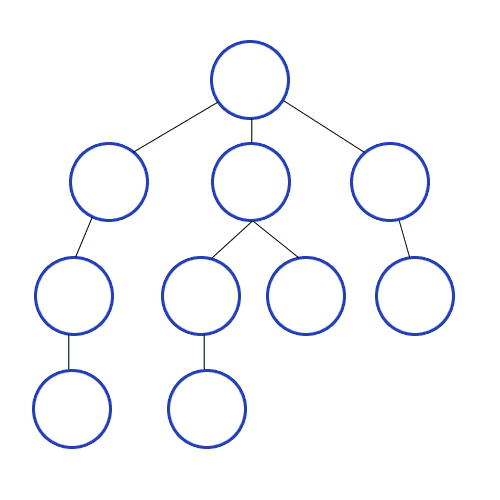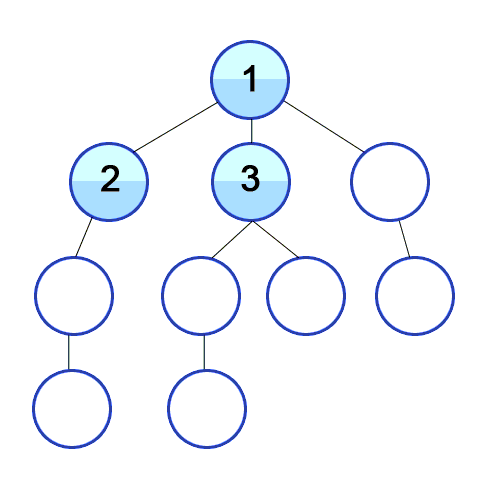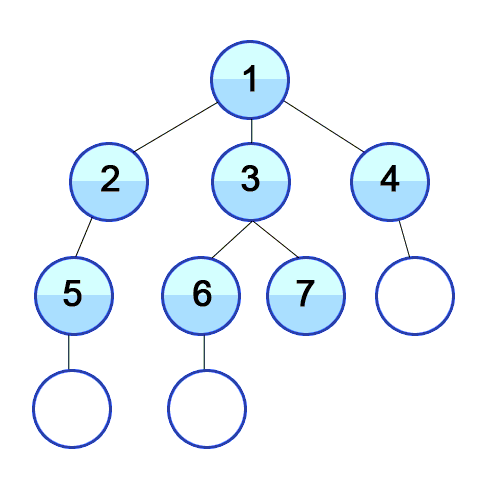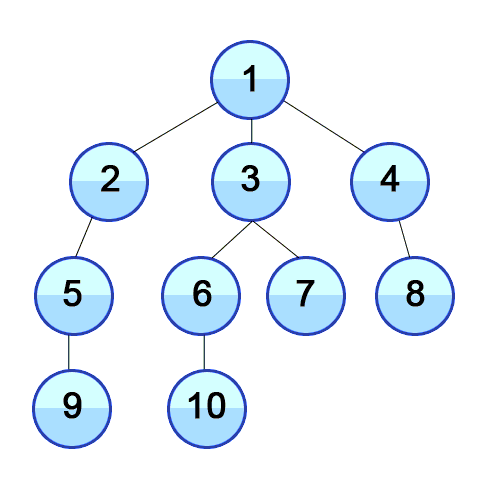
신장 트리 (Spanning Tree) ? 

하나의 그래프가 있을 때 그 그래프의 모든 노드를 가지고 있으면서 사이클(Cycle)이 없는 부분 그래프(Sub graph)!

원래 그래프가 N개의 노드를 가진다면, 그 놈의 신장트리는 N개의 노드와 N-1개의 간선(edge)를 갖는다. (간선이 N - 1개보다 적으면 모든 노드가 연결돼있지 않고 N - 1개보다 많으면 사이클이 있는 그래프다).

최소 신장 트리?

신장 트리는 원본 그래프의 부분 그래프이므로 당연히 여러 개 존재할 수 있는데, 그 중 간선들의 가중치 합이 가장 적은 신장 트리를 최소 신장 트리(MST, Minimun Spanning Tree)라고 부른다.

크루스칼 알고리즘?

주어진 그래프에서 최소 신장 트리를 찾는 알고리즘이다. 그리디 알고리즘의 일종으로, 이해하기 매우 쉬운 알고리즘이다. 

1. 가장 작은 가중치를 갖는 간선을 선택한다. 
2. 선택되지 않은 간선 중 가장 가중치를 갖는 간선을 선택한다
3. 그 간선이 기존에 선택했던 간선들과 사이클을 이루지 않는지 체크. 만약 사이클을 이룬다면 그 간선은 버린다.
4. 모든 노드들이 골라질 때까지 2 ~ 3을 반복

모든 노드들이 골라지는지의 여부는 노드들을 세도 되고, 선택된 간선의 개수가 N - 1개인지로 해도 되고, 아니면 그냥 모든 간선들에 대한 조회가 끝날 때까지 해도 된다. 매 페이즈마다 사이클을 이루지 않게끔 골라왔으니 이렇게 만들어진 서브트리는 신장 트리임이 보장되며, 또한 매 페이즈마다 항상 작은 가중치를 갖는 간선들을 골라왔으니 이렇게 만들어진 신장트리는 당연히 최소 신장 트리임이 보장된다.

가장 까다로운 작업은 사이클을 이루는지 판단하는 작업인데, 이는 유니온 파인드를 통해서 간단히 판별할 수 있다.

※ 유니온 파인드에 대해 정리했던 글

https://jofestudio.tistory.com/11

유니온 파인드로 사이클을 판별가능한 이유

유니온 파인드를 이용하면 무방향 그래프에서의 사이클 판별이 가능하다. 방향 그래프에서는 DFS를 통해 가능함. 근데 어떻게 가능한 걸까?

우선 다음 작업으로 사이클을 판단가능하다.

1. 간선을 고른다.
2. 그 간선들에 딸린(?) 노드 두 개가 있을 것이다. 그 두 놈이 같은 집합에 있는지, 즉 같은 그래프에 있는지 확인한다.
3. 두 놈이 다른 그래프에 있다면 두 노드에 대해 Union연산을 한다. 두 놈이 같은 그래프에 있다면 사이클이 있는 거다.

왜 이 작업으로 사이클 판단이 된다는걸까?

유니온 파인드는 집합에 대한 연산들로 생각할 수 있다. 유니온은 두 집합을 합치는거고, 파인드(흔히들 getParant라는 이름으로 메서드를 짓기도 함)는 특정 원소가 속한 집합을 알려주는 연산인 거다. 여기서, 그래프를 일종의 집합으로 볼 수 있다!

이 그래프에서 가장 작은 노드를 리더로 생각한다면 어떨까. 그럼 위 그래프에서의 리더는 0이다. 

1이 속한 그래프의 리더 = 0 이다.

5가 속한 그래프의 리더 = 0 이다.

이런 식으로, 그래프를 하나의 집합으로 표현가능한 것이다. 

이 그래프에서, 우선 처음에 다음과 같이 리더 테이블을 만들어줬다고 하자. 육안으로 세 놈이 같은 그래프에 있는 걸 당연히 확인가능하지만 일단 각자가 서로 다른 그래프에 있다고 생각하고 테이블을 초기화한다.

간선 (1, 2)를 골랐다. 두 노드가 같은 집합에 속하는지(즉 두 놈이 속한 집합의 리더가 같은지)를 보니까, 다르다. 그럼 두 놈을 Union해준다.

즉 이제 노드 1과 노드 2는 같은 집합, 즉 같은 그래프에 있다고 생각할 수 있다.

이번엔 간선 (1, 3)을 골랐다. 두 노드가 같은 집합에 속하는지를 보니까, 다르다. 그럼 두 놈을 Union해준다.

즉 이제 노드 1과 노드 3은 같은 집합 즉 같은 그래프에 있다고 생각할 수 있는 거다.

이제 간선 (2, 3)을 골랐다. 두 노드가 같은 집합에 속하는지를 보니까 같은 집합에 있다! 노드 2가 속한 집합의 리더와 노드 3이 속한 집합의 리더가 같기 때문이다. 따라서 처음에 그림으로 주어진 그래프가 사이클이 있다고 판별가능하다. 왜냐하면 간선 (2, 3)을 골랐다는 것 자체가 노드 2와 3은 서로 이어져있음을 의미하는 것이기 때문이다.

• 즉 노드 2와 노드 3이 서로 다른 집합이었다면, 이 둘을 이어도(둘 사이의 간선을 그린다고 생각) 사이클은 생기지 않음. 원래 둘이 속한 집합 즉 그래프가 겹치지 않는 것이었으니까!
• 그러나 노드 2와 노드 3이 서로 같은 집합이었다면..즉 둘 사이를 잇기도 전에 애시당초 같은 그래프 안에 있던 거라면 그 둘을 잇는다는 것은 사이클을 만드는 것이 되는 것임. 

따라서 유니온 파인드로 그래프의 사이클 판단을 내릴 수 있는 것이다.

그래서 크루스칼은 결국 다음과 같은 순서로 진행한다고 볼 수 있다

1. 가장 작은 가중치를 갖는 간선을 선택한다. 
2. 그 간선에 딸린 두 노드가 같은 집합인지 판단(즉 두 노드의 리더를 비교)
3. 같은 집합이면(두 노드의 리더가 같다면) 그 간선을 선택하지 않음. 5로 건너뜀
4. 다른 집합이면(두 노드의 리더가 다르면) 그 간선을 선택. 두 노드는 union연산해줌
5. 그 다음으로 작은 가중치를 갖는 간선을 골라 2부터 반복. 모든 노드들이 골라질 때까지!

브루트포스 알고리즘은 사실 설명하기 민망할 수 있을 정도로 직관적이다. 가능한 모든 경우를 따져가며 답을 찾는 방식. 따라서 시간만 충분하다면 이 방식으로 찾은 답은 정답임이 보장된다. 모든 경우를 다 따져본 거니까..

ex - 1) 1부터 N까지의 합은?

: 무식하게 풀자면, 1부터 N까지 숫자들을 하나하나 다 더해보면 됨. 시간은 좀 걸리지만 100% 확실한 정답을 보장.

sum = 0
for i in range(1, N + 1):
	sum += N

ex - 2) 주어진 배열에 x라는 수가 있는가?

: 무식하게 풀자면, 주어진 배열의 원소를 순서대로 순회해보면 된다. 모든 원소를 순회해보면 있는지 없는지 100% 따질 수 있다.

N = 100

def solution(N, arr):
	for i in arr:
    	if i == N:
        	return True
    return False

이 방법의 최고 장점은 100% 확실한 답을 보장한다는 것. 그러나 단점은 시간이 오래 걸릴 확률이 매우 높다는 것! 

최근 알고리즘 스터디를 시작했는데, 문제를 푸는 방법에 대해 설명을 들었다. 다음과 같다.

1. 우선 무식하게 접근해보기. 즉 브루트하게 풀려면 어떻게 할 수 있나 설계해보기

2. 설계한 브루트 방식의 시간복잡도를 계산해보고, 주어진 문제의 시간제한 내에 풀 수 있을 것 같으면 코드로 옮기기

3. 시간 내에 풀 수 없을 것 같으면 다른 방식으로 해보기. 설계했던 브루트한 방식을 어떻게 최적화할 수 있을지도 고민하기.

참고로 c++언어는 대략 1억번의 연산을 1초 내로 할 수 있고, 파이썬 언어는 대략 5천만번의 연산을 1초 내에 할 수 있다고 한다. 따라서 설계한 브루트한 방식의 시간복잡도가 O(n^2) 뭐 이런 식으로 나왔다면, 여기에 문제에서 n의 최댓값으로 주어지는 값을 넣어봐서 시간 내에 충분히 될 것 같으면 코드를 짜보라는 것. 참고로 애매하게 음 한 1억번 정도 연산할 것 같은데? 로 되지는 않고 100억번 정도  연산하네? 또는 100만번만 연산하네? 정도로 확실하게 주어진다고 한다.

분리집합(Disjoint Set)이란 서로 중복되지 않는 부분집합들로 나뉜 원소들에 대한 정보를 다루는 자료구조이다. Union-Find 알고리즘은 이 자료구조를 활용하는 대표적인 그래프 알고리즘 중 하나로, '합집합을 찾는다'라는 의미를 가진다. 디테일하게 들어가면 원소 x, y를 고른 다음 x가 속한 집합과 y가 속한 집합이 같은지 판별하는 알고리즘안대, 이는 여러 노드가 존재할 때 내가 선택한 임의의 두 노드가 서로 같은 그래프에 속하는지 판별한다는 것과 같은 개념으로 생각할 수 있다.

그냥 내가 이해한대로 쉽게(나름대로) 설명하자면, Union-Find알고리즘과 분리집합은 집합을 표현하는 하나의 형태이다. 1부터 5까지의 원소들이 있고 이들이 각각 집합의 형태를 이루고 있다고 하자. 즉,

{1}, {2}, {3}, {4}, {5}

이렇게 있는 것이다. 근데 이를 표를 통해 다음과 같이 표현할 수 있다.

{1}의 입장에서 자기가 속한 집합의 리더는 자기 자신(1)이고, {2}나 다른 애들 입장에서도 마찬가지다. 즉 표를 통해 자신이 속한 집합의 리더를 나타내준것! 근데 여기서 {1}과 {2}가 만나서 합집합 {1, 2}를 만들어냈다고 하자. 1과 2가 같은 집합의 원소로 구성된 것이다. 현재 존재하는 집합들은

{1, 2}, {3}, {4}, {5}

인 것이다. 이는 방금과 같은 표를 통해 어떻게 표현할 수 있을까?

다른 건 변함없고 2만 변화가 생겼다. 자신이 속한 그룹의 리더가 1이 된 것! 사실 뭐 2를 리더로 할 수도 있지만..집합을 이루는 원소 중 가장 작은 놈을 리더로 뽑는 것이다. 쉽게 생각해서 2는 1이 이끄는 집합의 멤버가 된 것이라고 생각해도 된다. 만약 다른 애들도 서로 합치고 지지고 볶고 해서 집합들이 다음과 같이 됐다면?

{1, 2}, {3, 4, 5}

표는 다음과 같아질 것이다.

그럼 생각해보자. 내가 임의로 두 원소를 뽑았는데 그 놈이 2랑 4다. 이들이 각각 속한 집합은 같은가?

표를 통해서 다르다는 것을 알 수 있다. 왜 Why? 2는 1이 이끄는 집합에 속해있고, 4는 3이 이끄는 집합에 속해있기 때문이다. 서로가 속한 집합의 리더가 다르기 때문에 이들이 속한 집합은 서로 다른 집합이다라고 말할 수 있는 것이다. 이것이 Union-Find알고리즘이다. 

근데 Union Find알고리즘은 여러 노드가 존재할 때 두 노드를 선택해서 이 두 녀석이 같은 그래프에 속하는지 판별하는 것으로도 이해할 수 있다고 했다. 간단하다. 단지 집합으로 표현하던 걸 그래프로 나타낼 때 Union Find가 저렇게 표현될 뿐이다. 1~5까지의 각 원소들이 집합의 형태를 이루고 있는 상태를, 1~5까지의 노드들이 서로 연결되지 않고 존재하는 상태라고 이해하면 된다. 그리고 집합들이 합쳐지는 것은 노드들 간에 연결선이 생겨서 연결되는 것으로 생각하면 된다. 따라서 내가 고른 임의의 두 노드가 서로 같은 그래프에 존재하는지 확인하는 것은 각각의 root노드들을 확인해서 같으면 같은 그래프 상에 존재하는 것이다! ...사실 이 부분은 글로만 써서 이해가 잘 안 될 수도 있으니 공부할 때 참고한 나동빈 님의 영상을 링크로 걸어두겠다.

https://www.youtube.com/watch?v=AMByrd53PHM 

그럼 Union Find를 파이썬으로 구현해보자.

parant = [i for i in range(n + 1)]

def getParant(x):         # x의 부모를 리턴하는 함수
    if parant[x] == x:    # x의 부모가 자기자신이라면 x를 그대로 리턴
        return x        
    parant[x] = getParant(parant[x])  # x의 부모가 자기자신이 아님 -> 재귀호출로 x의 부모 재설정
    return parant[x]                  # 최종적으론 x의 부모 리턴
    
def union(x, y):        # x가 속한 집합과 y가 속한 집합 합치기 - 가장 부모을 비교해 더 작은 쪽으로 합침
    x, y = getParant(x), getParant(y)
    if x < y:           # x가 더 작으니까 y의 부모를 x로
        parant[y] = x
    elif x > y:         # y가 더 작으니까 x의 부모를 y로
        parant[x] = y

def hasSameParant(x, y):         # x, y가 같은 부모를 같는지 즉 같은 집합에 속해있는지
    x, y = getParant(x), getParant(y)
    if x == y:
        return "YES"
    else:
        return "NO"

리더로 표현하던 것을 부모로 표현하는 것에만 차이가 있다. getParant함수가 이 알고리즘의 핵심으로 자신의 부모가 자기자신이 아니라면 재귀호출을 통해 자신의 부모를 최상단 노드, 즉 집단 내에서 가장 작은 놈으로 설정해준다.  이를 통해 백준 사이트에서 대표적으로 다음과 같은 문제를 풀 수 있다.

https://www.acmicpc.net/problem/1717

그래프같은 걸 탐색할 때, 너비를 우선으로 탐색을 진행하는 것을 너비우선탐색, 영어로는 Breadth First Search라고 하며 줄여서 BFS라고도 부른다. 어떠한 시작점이 있을 때, 그로부터 가까운 것들부터 탐색해나가는 방법으로 맹목적인 탐색을 할 때 사용가능한 방법이다. 이 녀석은 '최단 경로'를 찾아주기 때문에 최단길이를 보장해야 할 때 많이 쓰인다.

예시)

이 방법을 구현하려면, 큐(queue)가 필요하다.

그럼 이걸 파이썬으로 구현해보자.

우선 그래프는 다음과 같이 딕셔너리 형태로 표현해봤다.

graph = {
    1 : [2, 3, 4],
    2 : [1, 3],
    3 : [1, 2, 4, 5],
    4 : [1, 3],
    5 : [3, 6],
    6 : [5]
}           # 키에 연결된 value에 있는 리스트가 그 key에 연결된 애들임

그리고 BFS를 도와줄 큐는 다음과 같이 해보자.

queue = []                       # 큐를 리스트 형태로 구현

queue.append(something)          # 큐에 요소를 넣는 동작 : append  ->큐의 뒤쪽에 추가
queue.pop(0)                     # 큐에 요소를 빼는 동작 : pop(0)  ->큐의 앞쪽에 있는 걸 뺌

 그럼 BFS를 다음과 같이 만들 수 있다.

def BFS(graph, start_node):
    visited = []                           # 방문한 요소들이 이 리스트에 저장됨
    queue = [start_node]                   # 큐

    while queue:                           # 큐에 뭔가 있는 동안 이하 내용을 반복한다
        node = queue.pop(0)                # 큐의 제일 앞에 있는 놈을 빼와서
        if node not in visited:            # 만약 이 놈이 방문한 적이 없다면
            visited.append(node)           # 방문처리
            print(node)                    # 그 녀석 출력
            queue.extend(graph[node])      # 그 녀석과 연결된 요소들(graph[node])를 queue에 추가

근데 이 방법에는 문제점이 있다.

그것을 확인하기 위해 다음과 같이 코드 중간중간에 print를 써서 현재 queue와 visited에 있는 값들을 하나하나 확인해보고,  걸리는 시간까지 알아보자.

import time

def BFS(graph, start_node):
    start = time.time()
    visited = []
    queue = [start_node]

    while queue:
        node = queue.pop(0)
        if node not in visited:
            visited.append(node)
            print(node)
            print(f'방문 처리 후 visited : {visited}')
            queue.extend(graph[node])
            print(f'큐에 연결된 요소 추가 후 queue : {queue}')
        print("-"*10)
    print(time.time()-start)

대략 0.007초가 걸렸다.

이 코드의 문제점은 그럼 뭘까?

어떤 요소를 방문처리해주고(visited.append(node))

그 요소와 연결된 요소들(graph[node])를 큐에 추가해줄 때, 방문한 적 없는 요소들만 추가해야 한다.

근데 위 코드는 일단 연결된 요소들 전부 큐에 추가해주고, 나중에 큐에서 꺼낼 때 꺼낸 값이 방문한 적이 있는지 없는지를 판단하기 때문에 쓸데없이 시간을 낭비하는 꼴이 된다.

그래서 다음과 같이 바꿔줄 수 있다.

def BFS(graph, start_node):
    visited = []
    queue = [start_node]

    while queue:
        node = queue.pop(0)
        if node not in visited:
            visited.append(node)
            print(node)
            for nd in graph[node]:             # 연결된 요소들에 대해 하나하나 따진다
                if nd not in visited:          # 방문한 적 없는 요소여야
                    queue.append(nd)           # 큐에 추가

그러나 이 방법도 문제점이 있다. 큐에 원소들을 추가해주는 작업을 하는 부분을 보면 graph[node]에 해당하는 리스트의 원소들을 루프문으로 돌기 때문에, 시간낭비가 역시 생길 수 있다!

이 문제점을, set이라는 자료형를 사용해 상당히 간편하게 해결할 수 있다.

그래서 다음과 같이 해준다.

def BFS(graph, start_node):
    visited = []
    queue = [start_node]

    while queue:
        node = queue.pop(0)
        if node not in visited:
            visited.append(node)
            print(node)
            queue += (set(graph[node]) - set(visited))

그러나 아직까지도 문제가 있다..ㅋㅋㅋㅋㅋㅋ

큐에서 제일 첫 번째 녀석을 빼주는 queue.pop(0)이 문젠데, 이 녀석의 시간복잡도가 O(n)이라는 것.

이는 collection 라이브러리에 있는 deque를 사용해 해결가능하다.

그리고 visited가 리스트로 되어있는데,

if in 또는 if not in방법은 리스트에서 하면 이 역시 시간복잡도가 O(n)이다.

따라서 visited를 딕셔너리 또는 집합(set)으로 해주는 게 더 빠르다!

그래서, 다음과 같이 해주자.

from collections import deque

def BFS(graph, start_node):
    visited = {}
    queue = deque([start_node])

    while queue:
        node = queue.popleft()
        if node not in visited:
            visited[node] = True
            print(node)            
            queue += (set(graph[node]) - set(visited))

누군가 x의 y승은 얼마인가? 라고 물었다. 그에 대한 대답은?

그냥 x ** y를 리턴하면 되긴 하지만(Python 기준), 그거 말고.

일반적으로는 다음과 같이 구할 수 있다.

def pow(x, y):
    answer = 1
    for i in range(y):       
    	answer *= x
    return answer

이 방법의 시간복잡도는 O(y)이다.

근데 더 빠르게 구할 순 없을까?

첨에는 단순하게, 저 방법은 루프를 y번 돌면서 하는거니까 루프횟수를 줄이면 된다고 생각했다.

만약 x의 y승을 구할 때 y가 짝수라면

x의 y승 = (x의 y/2승) * (x의 y/2승)

이고, y가 홀수라면

x의 y승 = (x의 y/2승) * (x의 y/2승) * (x)

이므로, 루프를 y번까지 돌 필요없이 y의 반 정도까지만 돌면 된다!고 생각해서 다음과 같이 코드를 짰었다.

def pow(x, y):
    answer = 1
    for i in range(y//2):
        answer *= i
    if y%2 == 0:                     # y가 짝수
        return answer * answer
    else:                            # y가 홀수
    	return answer * answer * 1

그러나 이것의 시간복잡도도 O(y)이다. y가 커질수록 y의 반까지만 루프를 돈다는 건 의미가 없어지기 때문..

그러나 이것의 시간복잡도를 O(lg y)로 줄일 수 있는 방법이 있다.

우선 거듭제곱을 구할 때 루프가 아니라 재귀로도 구할 수 있다는 점에 힌트가 있다.

다음과 같이 코드를 짜면 재귀의 방법으로 거듭제곱을 구할 수 있다.

def pow(x, y):
    if y == 0:
        return 1
    return x * pow(x, y - 1)

물론 저것의 시간복잡도 역시 아직은 O(y)임.

그러나 예를 들어서, 2의 8승은 다음과 같은 과정으로 구할 수 있다는 점에 주목하자.

2의 8승 = (2의 4승) * (2의 4승)

2의 8승 = ((2의 2승) * (2의 2승)) * ((2의 2승) * (2의 2승))

.....

즉 다음과 같이 가능하다는 말.

def pow(x, y):       
    if y == 1:
        return 1
    return pow(x, y//2) * pow(x, y//2)    # 물론 y가 짝수일 때만 가능

근데 같은 내용에 대해 재귀를 두 번 호출할 필요는 없으니, 다음과 같이 하는게 더 빠르다.

def pow(x, y):       
    if y == 1:
        return 1
    sub_answer = pow(x, y//2)
    return sub_answer * sub_answer    # 물론 y가 짝수일 때만 가능

아까 x의 y승을 구할 때 y가 홀수라면 x의 y승 = x의 y/2승 * x의 y/2승 * x라고 했었으니, y가 홀수일 때도 포함해 다음과 같이 완성 가능하다.

def pow(x, y):       
    if y == 1:
        return 1
    sub_answer = pow(x, y//2)
    
    if y%2 == 0:
    	return sub_answer * sub_answer    
    else:
        return sub_answer * sub_answer * x

이렇게 하면 O(lg y)의 시간복잡도로 거듭제곱을 더 빠르게 계산할 수 있다.

내가 한 거랑 뭐가 달랐던 걸까?

우선 기본적인 접근법은 같았던 것 같다. y가 짝수인지 아닌지에 따라, 2/y까지만 곱한 걸 다루는 면에서.

그러나 y가 만약 16으로 주어졌을 때, x의 16승은 x의 8승 * x의 8승이 맞긴 하지만 x의 8승을 구하는 것도 다시 반으로 쪼개서 할 수 있다는 점을 간과했다.