https://www.acmicpc.net/problem/11726
11726번: 2×n 타일링
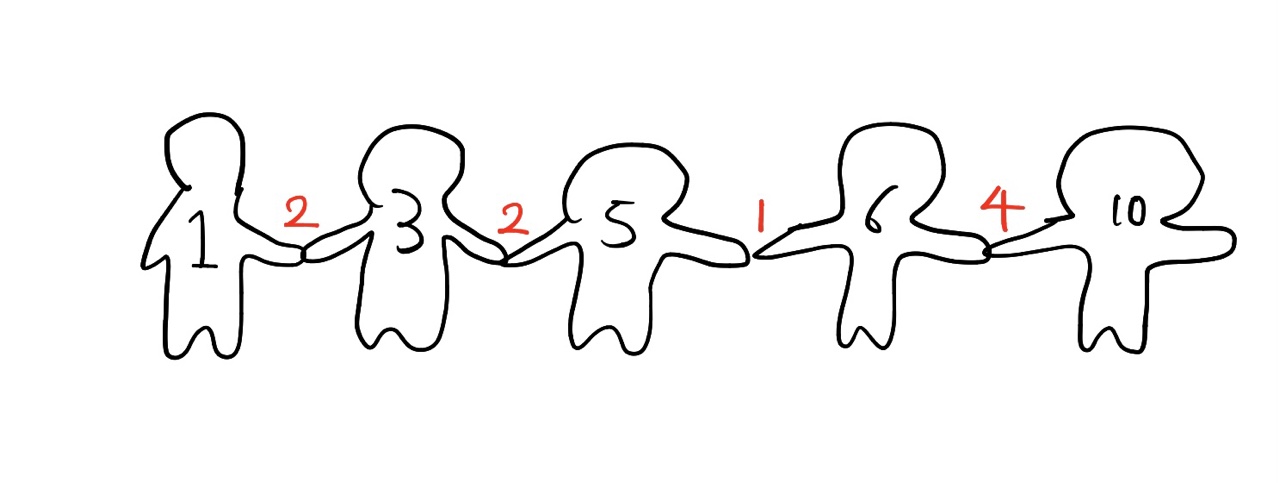
2×n 크기의 직사각형을 1×2, 2×1 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오. 아래 그림은 2×5 크기의 직사각형을 채운 한 가지 방법의 예이다.
www.acmicpc.net
1. 브루트 포스로 접근한다면
첫 번째 열부터 마지막 열까지 채운다고 할 때
지금 열을 세로블록으로 채울지
지금 열 + 바로다음열을 가로블록 2개로 채울지
를 선택함
러~프하게 생각하면 2^N개정도의 경우가 나오고 N은 최대 1000까지 주어지니 이 방법은 못 쓴다.
2. DP로 접근
k번째 열까지 채우는 것은
1) k - 2번째 열까지 채우고 세로블록 두 개 연달아 놓거나 가로블록 찍찍 놓거나
2) k - 1번째 열까지 채우고 세로블록 하나 놓거나
이 방법이다.
나는 여기서 k - 2번째 열까지 채우고 세로블록 두 개를 연달아 놓는 것과 k - 1번째 열까지 채우고 세로블록을 하나 놓는 것은 중복되는 것이 있으므로 그 부분을 처리하기 위해 공을 들였는데, 다 풀고 보니 예외처리할 필요가 없었다.
k - 2번째 열까지 채우고 세로블록을 두 개 연달아 놓는 행위가 k - 1번째 열까지 채우고 세로블록 하나 놓는 행위에 포함되기 때문.
k - 2번째 열까지 채우고 세로블록을 두 개 놓는 것을 동시에 놓는 게 아니라 하나하나 놓는다고 해보면, k - 2번째 열까지 채우고 세로블록을 하나 낳고 그 다음에 하나를 마저 놓는 것이지만 처음에 하나를 놓는 과정에서 이미 k - 1번째 열까지 채운 것이 된다는 것이다.
즉 k - 2번재 열까지 채우고 k번째 열까지 채우는 과정은 가로블록을 찍찍 놓는것만 생각하면 되는 것이었다.
일단 아쉬운 대로 내 풀이 공유..
N = int(input())
MOD = 10007
# dp[x][0] : x번째 열까지 채우는데 마지막이 세로로 끝나는 경우
# dp[x][1] : x번째 열까지 채우는데 마지막이 가로로 끝나는 경우
dp = [[0, 0], [1, 0], [1, 1], [2, 1]]
for i in range(4, 1001):
dp.append(
[(sum(dp[i - 2]) + dp[i - 1][1]) % MOD, sum(dp[i - 2]) % MOD]
)
print(sum(dp[N]) % MOD)
더 나은 풀이
N = int(input())
MOD = 10007
dp = [0, 1, 2, 3]
for i in range(4, N + 1):
dp.append((dp[i - 2] + dp[i - 1]) % MOD)
print(dp[N])느낀점
일단 이런 DP문제를 점화식을 세우는 과정에서 앗? 중복되니까 예외처리할 부분이 있는데? 라고 생각되는 부분들이 있다. k - 2번째와 k - 1번째에 어떤 연산?을 해주어 k번째를 구하는 경우, k - 2번째에서 구하는 것과 k - 1번째에서 구하는 것들이 새로 중복되는 게 있는 거 같은데? 하는. 그러나 k - 2번째에서 특정 연산을 하는 것을 유심히 보며 중간에 k - 1번째가 '되는' 부분이 있는지 봐야할 것이다. 그렇다면 그 부분을 빼고 생각하면 중복처리 땜에 머리 굴릴 필요가 없어지니까. 애시당초 k - 2번째와 k - 1번째에 서로 다른 종류의 연산을 가미해 중복될 일이 없도록 처음부터 생각하는 것도 방법일 듯하다.
그리고 굳이 처음부터 어떤 관계가 있을까 하며 뇌피셜로 점화식 세울라 하지 말고, 일단 2번째일땐 이 만큼의 가짓수, 3번째일땐 이만큼의 가짓수, 4번째일땐 이만큼의 가짓수..하면서 쭉 쓰다가 점화식 관계를 발견하는 것도 하나의 방법일 듯하다. 하나의 틀에 박히지 말자.
'ALGORITHM > 백준BOJ풀이' 카테고리의 다른 글
| [백준] 2075 - N번째 큰 수 (0) | 2023.01.27 |
|---|---|
| [백준] 1026 - 보물 풀이 및 그리디 정당성 검증 (0) | 2022.03.17 |
| [백준] 13305 - 주유소 풀이 (0) | 2022.02.09 |
| [백준] 13164 - 행복 유치원 파이썬 풀이, 자세한 풀이와 함께 (0) | 2022.01.29 |
| [백준] 11660 - 구간 합 구하기 5 by python (0) | 2022.01.08 |