어떠한 데이터들이 주어졌다. 이해를 돕기 위해 이 데이터들은 각각 1개의 원인 x와 1개의 결과 y를 가진다고 하자. 그럼 다음과 같이 좌표평면에 나타낼 수 있다.
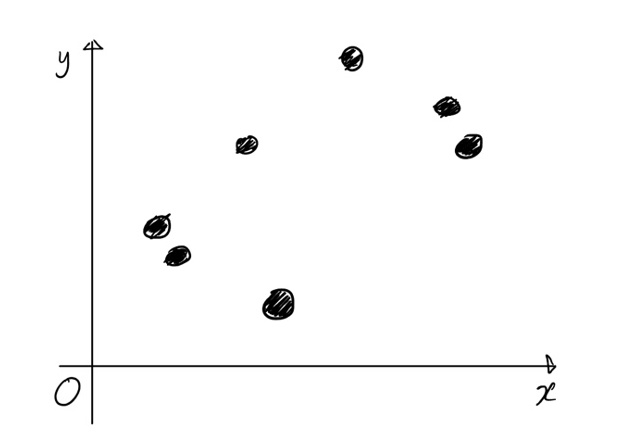
그리고 이 데이터(검은 점들)을 대표하는 선이 있다고 하면 어떨까?
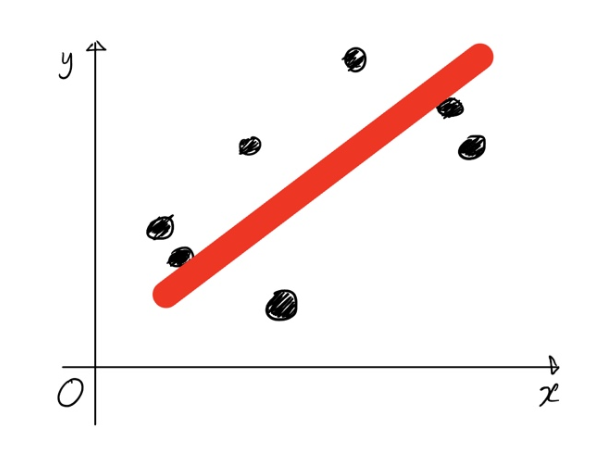
이 선을 이용한다면, 우리가 가지고 있지 않은 데이터가 있다고 해도 그 데이터의 x값을 이용해 y값을 예측해낼 수 있다.
그러나 과연 어떤 선이 '이 데이터들을 대표하는 선'이라 할 수 있느냐는 문제에 직면하게 된다. 이 선도 저 선도 어제 그은 그 선도 다 대표하는 선이라고 갖다 붙일 수 있을텐데 말이다. 이 때, 이 데이터들을 대표하는 선을 다음과 같이 정의한다면 어떨까.
"실제 데이터와의 오차들의 합이 가장 작은 선"
이렇게 되면 무수히 많은 선들 중 이 데이터를 대표하는 선은 딱 하나가 된다. 실제 데이터과의 오차란, 같은 x에 대해 내가 그은 선에서의 y값과 실제 데이터의 y값과의 차이를 의미한다. 따라서 임의의 직선 y = ax + b가 있을 때, 실제 데이터들과의 오차들의 합이 가장 작게 되는 a와 b를 찾게 된다면 이를 통해 임의의 x값에 대한 y값을 예측 가능하다. 이를 선형 회귀라 하며 영어로는 Linear Regression이라 한다.
참고 : 실제 데이터와의 오차들의 합이 가장 작으면 실제 데이터와의 오차 평균이 가장 작은 선이라고 할 수 있다. 또한 엄밀하게 말하자면 오차들은 양수가 될 수 있지만 음수가 될 수도 있으므로 오차합을 따지는 건 적절치 않다. 따라서 오차의 제곱들의 평균이 제일 작게 되는 선이라고 표현하는게 정확하다. 아니면 뭐 오차의 절댓값의 합이 가장 작은 이렇게 편하게 가도 되고..
그럼 관건은 이 a와 b값을 도대체 어떻게 찾느냐는 것이다. 최소 제곱법이란 공식을 통해 기울기 a와 y절편 b를 바로 구할 수 있는 방법이 있지만 세상은 그리 녹록치 않다. 방금까지는 일차함수 y = ax + b꼴만을 얘기했으니 원인에 해당하는 값이 1개인 경우만 본 거지만 실제 세상은 하나의 원인만으로 결과가 만들어지지 않기 때문이다. 즉 최소 제곱법으로 a와 b를 직빵으로 구하는 방법을 쓰기엔 처리해야할 입력값들이 너무 많은 것.
그럼 도대체 어떻게 a, b를 찾으라는 건데? 그건 바로
"일단 선 하나 그어봐. 그리고 수정해 나가자고"
이거다. 가설을 하나 세운 후 이 가설이 주어진 요건을 충족하는지 따져보고, 조금씩 수정해보며 변화가 긍정적인 쪽으로 수정해나가며 오차가 최소가 될 때까지 반복해보는 것. 이것을 하는 대표적인 방법으로 경사하강법이 있으며, 이는 다음 글에서 소개하겠다.