※ 아래 영상을 보고 개인공부를 위해 정리할 겸 작성한 글입니다.
https://www.youtube.com/watch?v=6fc9NAQkcv0&t=4s
원작자의 허락을 받았으며, 문제가 될 시 본 글은 삭제조치하겠습니다 :)
1. DNS란 무엇인가?
Domain Name System의 줄임말이다. www.naver.com이란 란 url이 있을 때, naver.com이 도메인에 해당하고 www는 호스트 네임에 해당하는 부분이다.
2. 근데 잠깐! 도메인은 왜 있는거야?
우리가 어느 웹사이트에 들어가려 하면, 우리가 쓰는 웹 브라우저(ex : 크롬, 사파리 등)이 그 사이트를 제공하는 지구의 어딘가에 있는 서버에다가 요청 즉 request를 해야 한다. 이를 위해선 이 서버의 IP주소를 알아야 한다. 그런데 사실 모든 웹 사이트의 IP주소를 하나하나 외우고 다니는 건 힘드니까..친구들 전화번호 하나하나 외우기 싫어서 전화번호부 만드는 것처럼, 이 IP주소들을 key : value처럼(전화번호부 예로는 친구이름 : 전화번호) 특정이름 : IP주소 관계로 만들면 좋겠다고 사람들이 생각한거지. 여기서 특정이름에 해당하는 부분이 도메인.
3. 도메인을 IP주소와 대응시킨 거구나. 그럼 이 '전화번호부'가 저장되는 곳이 따로 있어?
그게 바로 DNS! 근데 System이란 말에서 알 수 있듯이 이 전화번호부가 어느 한 군데에 싹 몰려 있는게 아니다! 다층적으로 구성된 네트워크에 분산되어 있다.
4. DNS의 동작원리 간단하게 한 입
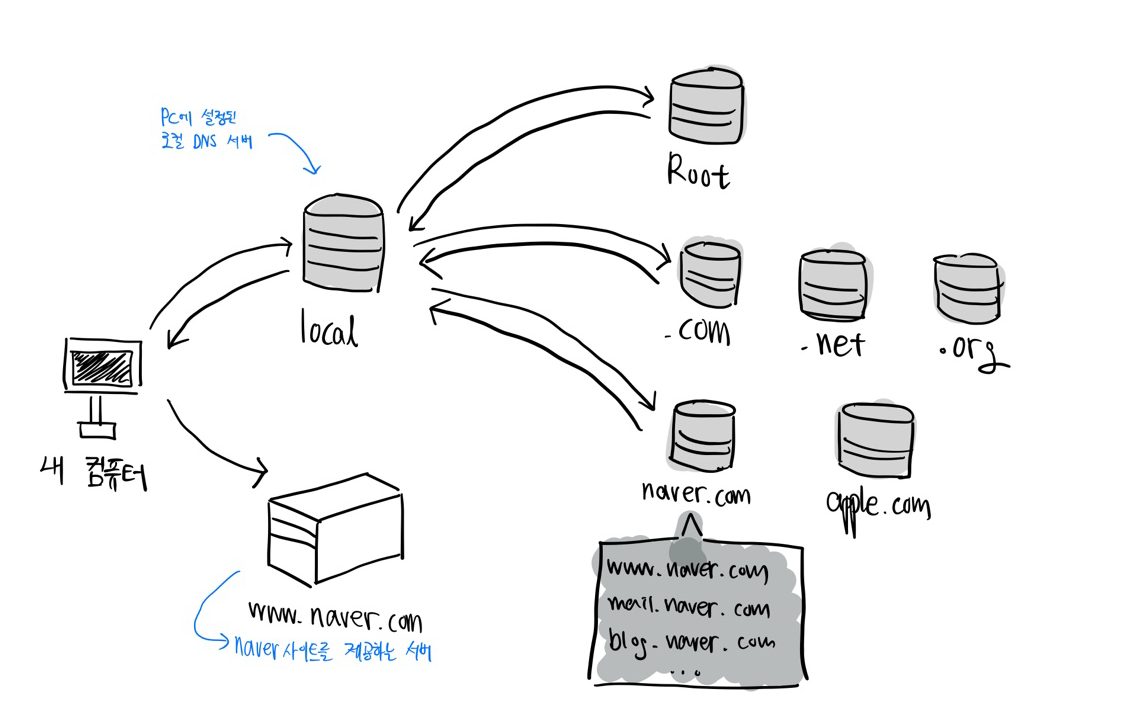
내 컴퓨터에서 www.naver.com에 에 접속하려는 상황이라고 하자. 그러면 naver사이트를 제공하는 서버에다가 request를 해야 하는데 그 서버의 IP주소를 현재 모르는 상태다! 이 때 브라우저는 PC에 설정된 로컬 DNS서버에 naver.com이라는 도메인과 www이라는 호스트 네임을 가지는 IP를 갖고 있는지 물어본다. (이 때 로컬 DNS서버는 통신사마다 다르며 사용자가 다른 곳으로 바꿀 수도 있음) 이 로컬 DNS서버엔 내가 원하는 IP주소가 이미 캐싱(caching)돼있을 수도 있고 아닐 수도 있는데, 캐싱돼있다면 바로 그 주소를 가져다가 쓰면 되고 없다면 다른 곳을 거쳐서 가져와야 한다.
여기서 '다른 곳을 거쳐오는 작업'은 우선 첫 번째로 Root DNS 서버에 이 주소(www.naver.com)에 해당하는 IP주소를 어디서 찾을 수 있냐고 물어본다. Root DNS 서버는 이에 대한 응답(response)로 .com으로 끝나는 도메인들을 담당하는 DNS 서버의 IP주소를 돌려준다! 이를 통해 로컬 DNS서버가 .com을 담당하는 DNS 서버에게 찾아가 내가 원하는 주소의 IP주소가 어딨느냐고 물으면, .com 담당 서버는 이에 대한 응답으로 naver.com의 도메인 정보를 가진 서버의 IP주소를 준다! 다시 이를 통해 로컬 DNS 서버가 naver.com의 도메인 정보를 가진 DNS 서버에게 찾아가고, 거기엔 여러 호스트 네임별(www, mail, blog 등)로 IP주소가 있는데 그 중 www와 매칭되는 IP주소 즉 www.naver.com의 IP주소를 준다. 이를 로컬 DNS서버가 브라우저에게 반환하면 비로소 www.naver.com의 의 서버로 접속하게 되는 것.
(개인적으론 컴퓨터 구조 시간에 배운 메모리, 캐시 등의 관계가 DNS서버간에도 있다는 게 신기했다)
5. 아니 그러면 DNS 서버들에 문제가 생기면 인터넷도 못하는거야?
Yes. 정확히 말하자면 DNS서버들에 문제가 생기면 전화전호부를 못 쓰게 되는 것이니 도메인을 통한 접속만 안되는 거고, IP주소를 안다면 그것을 활용한 접속이 가능. 그러나 IP주소로 직접 접근하는 걸 막아놓은 사이트는 아예 못 쓰는 것이 된다.
6. 가만 생각해보니, 해커가 DNS를 해커가 악의적으로 조작할 수 있을 것 같아
맞다. 해커가 악의적으로 내가 원하는 사이트의 IP주소가 아니라 다른 엉뚱한 사이트의 IP주소를 알려주도록 할 수 있다. 이를 DNS 스푸핑(DNS spoofing)이라 함!
7. 근데 로컬 DNS서버를 바꾼다는 건 뭐야?
로컬 DNS서버는 일반적으로 통신사 것으로 설정돼있는데, 이걸 수정한다는 것은 정부에서 막아놓은 사이트에 접속하거나 국가검열받은 전화번호부 대신 외국의 전화번호부를 쓴다는 것과 같은 의미! 또는 특정 서비스를 보다 빠르게 이용하기 위해 로컬 DNS서버를 바꾸기도 함. 예를 들어 기본 로컬 DNS서버를 구글의 서버 주소로 세팅하면 유튜브처럼 구글에서 제공하는 서비스를 보다 빠르게 이용가능! (그러나 다른 서비스들은 느려질 수 있으니 그냥 쓰던 대로 쓰자..)
'WEB > 그 외 필요한 지식' 카테고리의 다른 글
| [짧] 단방향 암호화 vs 양방향 암호화 (0) | 2023.01.24 |
|---|---|
| 세션 인증 방식 vs 토큰 인증 방식 (2) | 2023.01.24 |
| HTTP 상태 코드 (0) | 2022.07.12 |
| HTTP의 특징(stateless 등..) (0) | 2022.07.06 |
| JWT(JSON WEB TOKEN) (0) | 2022.06.22 |







